Welcome back! Chapter 7 of Guided Math in Action is all about building students' mathematical proficiency and how guided math is the ideal framework for doing so.
Dr. Nicki outlines the five components of mathematical proficiency and how to teach each. I have included a summary of each, as presented by Dr. Nicki, and have shared a bit about how each is developed in my classroom--ultimately answering the discussion questions for chapter 7 as well.
Conceptual Understanding---Understanding how to do something on a conceptual level
What does it look like in a guided math group?
- Use of manipulatives, scaffolds, and tools
- Modeling/demonstrating by teacher
- Opportunities for students to work together as a group, with partners, and independently
- Debriefing as a group at the end of lesson
Common Core: Much focus on knowing what a concept means not just knowing how to do something
I use various tools to help students develop conceptual understanding. In the photo below, you can see the place value tools I use with my students. Not all tools are used by all students at the same time. Differentiation of tools is important in my guided math groups. For example, place value discs are only used with students after they have a firm understanding of their value (these tools are all sized the same and are labeled with the value). On the other hand, base ten tools are partitioned and sized according to their value providing a more concrete representation. Each tool has its own purpose and we learn about their benefits/limitations and appropriateness. You can download FREE place value disks, place value arrows, and ten frame tools by clicking here!
Procedural Fluency---Understanding how to do mathematical procedures
What does it look like in a guided math group?
- Students using conceptual knowledge to do the math
- Students using different methods to compute (writing, mental math, calculators, computers, manipulatives)
Common Core: Stresses the use of conceptual understanding to work on procedures
Once my students develop conceptual understanding of a skill, it's time to put that understanding to work. Multiple methods are always stressed. In the photo below, you will see how two pairs of students applied their understanding of using an open number line to two different problem situations. When faced with the problem, the students followed various steps. They identified what was known and what was unknown, wrote an equation to represent the situation, solved using a strategy of choice (open number line)m, and wrote their solutions in a sentence. In this case, both pairs of students chose to use an open number line to solve similar problems.
Strategic Competence---Ability to solve problems and represent thinking
What does it look like in a guided math group?
- Students solve problems with models
- Students represent their thinking (using numbers, symbols, words, and pictures)
- Students model/represent their thinking in multiple ways with discussion of the process and effectiveness (What do you think about how _____ solved? Who can explain what _____ did?, etc.)
Common Core: Standard for Mathematical Practice 4 -- Students need to find pathways rather than just jumping to a solution and use various models to explain their thinking.
Once students have learned multiple ways (pathways) for working through a problem, they begin to choose what works best for them. They also begin to understand that some ways/tools are not as efficient as others. For example, if a problem situation requires combining two values, 346 and 543, a ten frame model would work but would not be most appropriate/efficient. As students work through a multitude of problem situations, they begin to see the relationship between models/ways of representation. This enables them to look at their fellow classmates' "pathways" and understand their thinking. In the photo below you will see a student represented his thinking in two ways (base ten and mental addition of tens and ones).
Adaptive Reasoning---Ability to think logically about math and explain and justify
What does it look like in a guided math group?
- Students discussing in a safe environment where their ideas are valued
- Students listening, making connections, asking questions
- Students proving their thinking (using more than one method) and comparing/contrasting their methods, and evaluating the reasonableness of methods
Common Core: Content standards and practices require reasoning ("explain", "justify", "assess the reasonableness")
I shared my problem solving discussion fans in a previous post, but they are definitely useful in guiding student discussion away from the teacher and in small guided math groups. My kids love these little buggers---the depth of their discussions and the affirmation given to one another is amazing. Students begin to understand the different types of questions that can be asked, and I often hear students asking thoughtful questions without the fans as the year progresses. For more information about how I use discussion fans with my students, download them here!
Mathematical Disposition---Ways of thinking, doing, being, and seeing math
What can teachers do?
- Provide scaffolded problems that students can solve successfully
- Talk about more than one way to do something
- Engage students in discussions of how they got an answer, not just the correct answer
- Give students the time to think, reason, and even struggle with a problem (with the understanding that struggling is sometime necessary before being successful)
- Promote stick-withitness
- Make connections to real-life
- Provide opportunities for student reflection and the monitoring of their learning
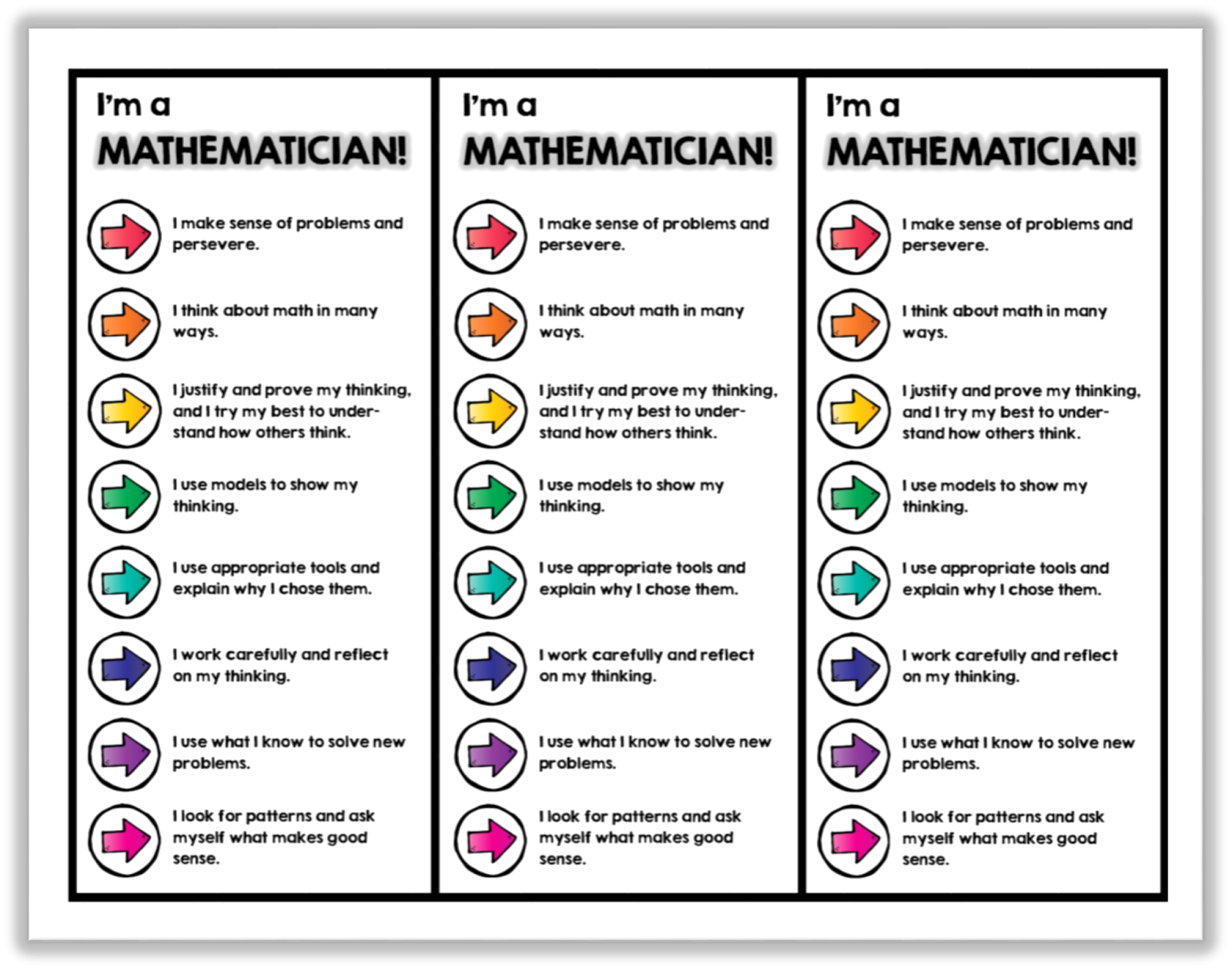
As a teacher, I strive to do all of the above! It's all about perseverance, the celebration of successes, making connections, and multiple ways of understanding. One of the most powerful things I try to do from the first few days of school is help students see themselves as mathematicians. This involves a beautiful discussion of what a mathematician is and what he/she does. We create an awesome anchor chart with all of our ideas spilling over--I held on to last year's anchor chart, but I will have to share a picture later (it's packed away at school). :0) This year, I also created a bookmark for the kids to keep in their guided math folders. It has all of the Common Core Practice Standards stated in simple, yet specific, terms. Please feel free to download a copy here!
The implementation of the Common Core Standards for Mathematical Practice are vital in students' development of mathematical proficiency. Here is an excellent teacher resource dedicated entirely to implementing the standards--Putting the Practices into Action by Susan O'Connell and John SanGiovanni. It's a must have and well worth the investment! Click here to learn more!
Such a significant chapter! I look forward to hearing how you help your students develop mathematical proficiency---please feel free to share in a comment! PLEASE! :0) You can also read past book study posts by clicking HERE!
All the best--
AND don't forget about our Dr. Nicki Newton, Problem Solving with Models, giveaway! Click here to check out these awesome resources! The lucky winner will get to pick the grade level resource that best fits him/her. We will be randomly drawing the winner next Sunday, August 3... Good luck!
a Rafflecopter giveaway